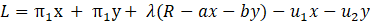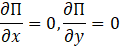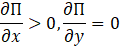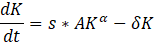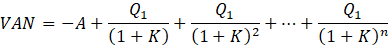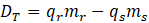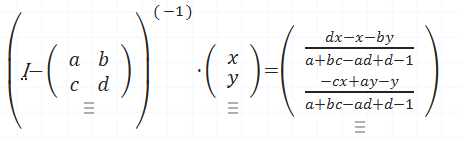¿Ganan demasiado las empresas? Claves económicas para entender el desempleo español

Contra la narrativa fácil: lo que realmente explica el estancamiento laboral

En los últimos años, diversas voces del pensamiento económico y político de izquierda en España —como Pablo Iglesias, Eduardo Garzón y Vicenç Navarro— han coincidido en señalar que el modelo económico dominante, de corte neoliberal, ha permitido a las grandes empresas alcanzar niveles elevados de ganancia a costa del bienestar colectivo. Desde sus respectivos enfoques, estos autores sostienen que la concentración de beneficios empresariales no ha sido acompañada por una redistribución efectiva, ni ha servido para mejorar de manera sustancial el empleo, los salarios o el acceso a derechos sociales básicos.

Iglesias plantea que el desempleo estructural, la temporalidad y la precarización del trabajo son síntomas de un sistema que favorece la acumulación en manos de unas pocas corporaciones, muchas de las cuales tributan por debajo de su capacidad real. Garzón, por su parte, defiende la idea de que el Estado debe asumir un papel más activo en la garantía de empleo, pues confiar en la lógica del mercado ha derivado en la exclusión de miles de personas del trabajo digno. Navarro, desde una perspectiva más estructural, acusa al neoliberalismo de haber debilitado deliberadamente el Estado del bienestar, otorgando privilegios fiscales y políticos a las élites económicas y financieras.

Estas tesis coinciden en una hipótesis central: que las altas ganancias empresariales, lejos de ser un motor automático de progreso social, operan bajo reglas que impiden su redistribución y perpetúan desigualdades. El presente artículo examina críticamente esa premisa, cuestionando hasta qué punto dichas ganancias son responsables de los problemas estructurales del mercado laboral español, y si existen factores alternativos —económicos, institucionales o culturales— que deben también considerarse en el diagnóstico.

La dinámica de las ganancias

Para comenzar con la respuesta, vale la pena iniciar con conceptos claves en la economía empresarial. En primer lugar, comprender lo que es un coste variable y los costes fijos. En el análisis económico de cualquier empresa, los costes se dividen habitualmente en dos grandes categorías: fijos y variables. Los costes fijos son aquellos que permanecen constantes independientemente del nivel de producción o actividad, como el arriendo de instalaciones, los sueldos administrativos o los seguros; es decir, deben pagarse incluso si no se produce nada. En cambio, los costes variables cambian en función del volumen de producción: aumentan cuando se produce más y disminuyen cuando se produce menos. Ejemplos típicos de este tipo de costes son las materias primas, el consumo de energía o los salarios por horas trabajadas en producción. Esta distinción resulta clave para entender la estructura de costes de una empresa y tomar decisiones sobre precios, escalabilidad y rentabilidad.

La relevancia de estos conceptos está en comprender cuánta debe ser la producción de un bien determinado -el bien que la empresa vende al mercado- para que la rentabilidad sea positiva.

Si establecemos que,

Donde «p» es el precio, C_V es el coste variable C_F el coste fijo, X es el punto muerto, que marca el umbral de producción y venta bajo el cual la rentabilidad se vuelve nula y negativa.

Supongamos que los costes variables son $ 5, el precio es $ 10 y el coste fijo $ 1000, el punto muerto será 200, lo que significa que recién con la unidad número 200 que se encuentre vendida los costos fijos serán sufragados, cada unidad vendida sobre la número 200 generará un beneficio positivo en la empresa, tal y como se puede observar en el gráfico que presento a continuación.

En cambio, si incrementamos los costos variables en 3 U.M., el punto muerto aumenta a 500 unidades monetarias. Sin embargo, se puede argüir que es posible mantener un nivel de rentabilidad si se incrementa el número de ventas, ante esto hay una serie de objeciones a realizar.

En primer lugar, los factores de producción no son ilimitados ni su oferta únicamente depende de las necesidades de la empresa. A una oferta limitada se deben sumar unos costes de adquisición y consumo que no necesariamente son constantes o decrecientes, al contrario, podrían ser crecientes.

Asumamos que poseemos los siguientes factores de producción (el trabajo es un factor de producción más):

Nuestra empresa produce X e Y, cada unidad del primero contribuye en 12 u.m. al beneficio de la empresa. El segundo tiene una contribución unitaria de 9 u.m. Para elaborarlos, la empresa utiliza 3 factores de producción que se recogen en la tabla anterior. Las cantidades máximas disponibles son 10 u.f. (unidad física) del primer factor, 21 del segundo y 32 del tercero.

Si queremos saber cuál debe ser la cantidad a fabricar en cada año para maximizar el beneficio de la empresa, la programación lineal es idónea para resolver el problema.

Siempre sujetos a la no negatividad de las variables X₁, X₂, …, X_n ≥ 0.

En este caso, por ende, el problema se expresa como sigue:

· Max Z = 12x + 9y

· X + y ≤ 10

· 3x ≤ 21

· 4x + 2y ≤ 32

· x, y ≥ 0

La solución a este problema, como es uno que incluye solo dos variables, se puede presentar (y resolver) gráficamente:

En este caso, el máximo de beneficio alcanzable en la zona plausible de producción (todo el espacio bajo las rectas) es 108, con los puntos x = 6, y = 4. En este caso, la posibilidad de incrementar el beneficio depende de la disponibilidad de las cantidades disponibles, por lo que eventualmente podríamos incrementar ilimitadamente el beneficio si las restricciones desaparecieran o se relajasen continuamente. Esto es lo opuesto a lo ya dicho, estamos dando vueltas en una misma idea pero retocarla sirve para avanzar a otro escenario: funciones de producción o ingreso con rendimientos decrecientes y funciones de costos con rendimientos crecientes.

Por ejemplo, si definimos la función de beneficios como sigue, 200x + 500y + 1,5xy − 1,5^x - y² + 10000, con x e y precios de dos productos que la empresa vende, podemos verificar una serie de hechos, entre otros podemos observar que es una función con rendimientos decrecientes ya que su segunda derivada es negativa, si queremos optimizarla, el punto en el que esta alcanza su máximo es (920/3, 480).

En este caso, obsérvese que cualquier solución que no sea el punto indicado previamente, nos entregará un resultado inferior a 241.000, por lo tanto, en estas condiciones (función de beneficios con rendimientos decrecientes), por lo que podemos comprobar que en este caso no es posible, ante un incremento de costos (por ejemplo aumento salarial), recuperar el margen mediante un incremento de producción.

La función de beneficio está definida tal y como sigue,

La cual, está compuesta por la función de ingreso R(x) y la función de costes C(x). Si nos encontramos con una función de beneficios con rendimientos constantes o crecientes eso significa que aplicar más factores productivos (en este caso x) redundará en un incremento constante o creciente del beneficio. Esto a priori podría parecer normal y esperable, pero en realidad mientras el ingreso tiene un rendimiento decreciente (más inversión en factores implica un resultado menor en el tiempo), el costo es constante o creciente. Piénsese en uno de los factores de producción más relevantes, el trabajo, invertir en más trabajo no tiene por qué repercutir en un incremento constante del output pero sí sabemos que el costo del trabajo se incrementa, y que, conforme la tasa de desempleo se acerca a un umbral mínimo los costos laborales tienden a incrementarse rápidamente.

Incluso podemos complicarnos más la existencia y establecer una función de beneficios y con restricciones de tipo KKT tal y como se presenta a continuación:

· Π (x, y) = px(x) + py(y) – C (x, y) → π₁x + π₁y

Donde px y py son los precios de x e y respectivamente, por lo que π_i = p_i - c_i . Además, tenemos de restricción de recursos:

· x > 0, y > 0

· g (x, y) = ax + by – R ≤ 0

Siendo R, el recurso disponible para el ciclo productivo.

Definimos entonces el lagrangiano:

Derivamos parcialmente:

De esto tenemos 8 escenarios posibles a analizar:

Analizando cada uno de estos escenarios llegamos a los siguientes resultados:

Caso 1:

x > 0, y > 0, g (x, y) < 0, λ = 0.

Válido si no hay ganancia marginal neta. Óptimo si π₁ = π₂ =0.

Caso 2:

x > 0, y > 0, g (x, y) = 0, λ < 0.

Válido y óptimo en el caso de que ambos bienes tengan igual rendimiento marginal por recurso.

Caso 3:

x > 0, y = 0, g (x, y) < 0, λ = 0

Inválido, se deja de producir y.

Caso 4:

x > 0, y = 0, g (x, y) = 0, λ < 0

Por lo tanto, para que u₂ > 0,

Válido si y es menos eficiente que x. Óptimo si conviene producir solo x.

Caso 5:

x = 0, y > 0, g (x, y) < 0, λ = 0

Inválido, se dejaría de producir x.

Caso 6:

x = 0, y > 0, g (x, y) = 0, λ < 0

Por lo tanto, para que u₁ > 0,

Válido si x es más rentable que y pero se escoge este último. Óptimo si y es más eficiente en uso de recursos.

Caso 7:

x = 0, y = 0, g (x, y) < 0, λ = 0

Contradicción.

Caso 8:

x = 0, y = 0, g (x, y) = 0, λ < 0

No se produce nada aun cuando el recurso se usa totalmente, lo cual es absurdo.

Bajo el supuesto de una función de beneficio estrictamente cóncava, con rendimientos marginales decrecientes, y restricciones lineales que representan la disponibilidad limitada de recursos, el análisis mediante el método de Kuhn-Tucker permite demostrar que el uso de los factores tiende al nivel óptimo. En particular, la solución que satisface las condiciones de primer orden de Kuhn-Tucker asegura que el ingreso marginal generado por cada factor de producción se iguala a su costo marginal total, que incluye no solo el costo directo sino también el valor sombra del recurso limitado. De este modo, se garantiza una asignación eficiente de los factores, ajustada a su productividad relativa y a las condiciones de escasez. Este resultado respalda la tesis de que, en contextos competitivos y con restricciones bien definidas, los agentes económicos utilizan los recursos de manera que maximizan su beneficio neto.

Este análisis se ve obstaculizado por una serie de supuestos contrarios que diluyen los presupuestos que fundamentan la tesis anterior: 1) la función de beneficio no necesariamente es cóncava, 2) la función puede tener saltos, por lo que las derivadas no serán continuas, 3) es un modelo que explica estáticamente los equilibrios, no es un modelo dinámico, no considera choques de precios, expectativas ni comportamiento intertemporal, 4) cuando hay fallas de mercado que tiendan a la formación de monopolios e información asimétrica, 5) cuando existen restricciones no convexas.

Analizaremos cada caso.

1) La función de beneficio no necesariamente es cóncava

En general esta crítica puede aplicar no solo a la función de beneficios sino también a otras como la función de producción o de ingresos. En ciertas condiciones, verbigracia economías de escala, los rendimientos pueden ser, y de hecho lo son, crecientes. Esto impone un grave problema para análisis como el que hemos realizado, sin embargo en el largo plazo estas funciones tienden a la concavidad pues se impone la ley de rendimientos decrecientes, y es que aun cuando una empresa pueda experimentar rendimientos crecientes en una etapa inicial (beneficio convexo), eventualmente enfrenta restricciones físicas, tecnológicas o de mercado que limitan su expansión eficiente. Del mismo modo, mantener niveles crecientes de producción implica costos crecientes, lo que irremediablemente transformará la función de beneficios en una función cóncava. Además existen imposiciones empíricas y sociales que llevarán a que estas funciones convexas con el paso del tiempo tiendan a la concavidad, uno de ellos es la misma competencia, la cual se traducirá en una pugna entre empresas que llevan a la reducción de precios y con ello una reducción de márgenes.

2) La función puede No Ser continua

Sí, funciones discontinuas no pueden ser diferenciables y por ende el teorema de Weierstrass no puede aplicar, pero esto no significa que el óptimo no exista. Por ejemplo si f(x) = 1 si x < 1 y f(x) = 0 si x > 1, tenemos claramente un óptimo máximo en cualquier punto menor que 1. Ahora bien, si la función discontinua, además es divergente, no existirá óptimo, por ejemplo f(x) = 1/x con x ϵ (0,1), no hay máximo ni mínimo en ese intervalo abierto, porque la función explota al acercarse a 0 y no está definida en el borde.

Esto último nos entrega la respuesta necesaria y suficiente para responder esta segunda crítica: en economía, las funciones que divergen (tienden a +∞ o −∞) no tienen un sentido real en economía por una serie de motivos, procederé a enunciar los más relevantes: primero, nadie puede incrementar su beneficio infinitamente, los recursos y factores de producción son finitos y por ende contradicen el principio de escasez.

3) Carece de una explicación dinámica

Cierto, no es un modelo dinámico, pero igualmente podemos establecer uno dinámico que llegue a conclusiones más o menos similares, planteemos la siguiente ecuación diferencial:

Supuestos:

· La inversión depende de la diferencia entre una tasa de retorno esperada y una tasa de depreciación natural.

· Cuanto mayor sea el retorno marginal del capital, más se invierte.

· Si el capital ya es muy alto, la rentabilidad baja → inversión se frena.

Donde:

· K(t): capital en el tiempo t

· s: tasa de ahorro/inversión (fracción del producto que se reinvierte)

· A: Productividad

· α: productividad marginal del capital (entre 0 y 1)

· δ: tasa de depreciación

· Producción: Y = AK^α

· Inversión: I = sY = sAK^α

· Depreciación: δK

· La diferencia entre inversión y depreciación da el cambio neto del capital

· dK/dt: cambio en el capital a lo largo del tiempo.

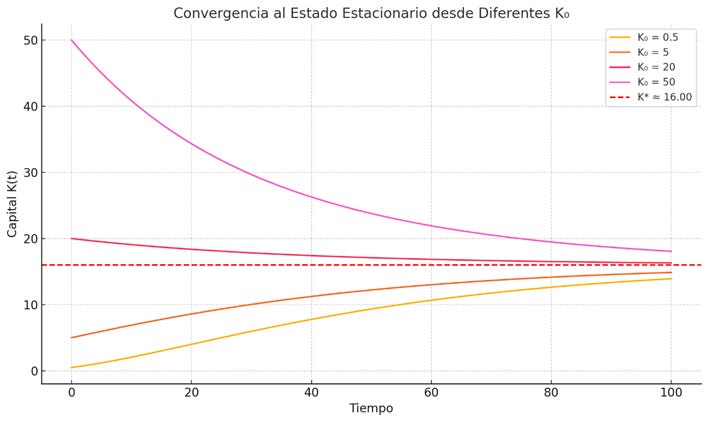
Este modelo es una simplificación del solowiano con fines ilustrativos para este artículo por lo que carece del elemento demográfico y tecnológico.

Cuyo resultado variará según el valor que tome α. Si establecemos un valor 0,5 entonces:

Esta es una solución explícita particular, lo importante es recalcar que si 0 < α < 1, podemos decir que el modelo tiende a un uso eficiente de los factores en el tiempo porque:

· Existen retornos marginales decrecientes del capital

· Existe un estado estacionario finito y estable

· Existen incentivos a invertir cuando hay poco capital, y desincentivos cuando hay mucho

Con estas condiciones el capital tiende al equilibrio y al uso eficiente y óptimo de los recursos en el largo plazo, tal y como se puede observar a continuación:

4) Las fallas de mercado, especialmente los monopolios e información asimétrica, también significan un obstáculo a la optimización.

En este caso, la existencia de monopolios con la capacidad de imponer precios elevados y un nivel de producción por debajo del óptimo. Debido a que estas empresas pueden fijar un precio muy por encima del costo marginal sin perder clientes terminan obteniendo rentas monopólicas, i.e, un tipo de beneficio económico que surge debido a la competencia restringida en la venta del producto de una empresa y que resultan de su posición como único proveedor de un bien o servicio.

Sin embargo, esta crítica se sostiene en la medida que los monopolios sean el resultado del desenvolvimiento económico dinámico, pero en condiciones de competencia, esto no debiera ser así. Si, la inversión tiende a los sectores con mayor nivel de rentabilidad e igualmente la desinversión tiende a darse en los sectores con menor rentabilidad, estableciendo como parámetro la media de beneficio, podemos construir una modelación formal del porqué los monopolios no tienden a imponerse.

Supuestos básicos:

· I_T: Inversión en el periodo T

· r_T: tasa de rentabilidad en el período T

· r*: tasa de rentabilidad media de la economía a largo plazo

· Si r_T > r* la inversión tenderá a aumentar

· Si r_T < r* la inversión tenderá a aumentar

· α > 0 es la velocidad de ajuste de la inversión ante cambios de los niveles de rentabilidad

· r_T – r*: es el incentivo a invertir o desinvertir

A la vez, el cambio de la inversión se puede expresar como sigue:

A su vez, podemos reescribir esta relación para encontrar el comportamiento de la rentabilidad a largo plazo,

Con

Donde podemos interpretar que,

· Si r_t > r* entonces ∆r < 0: la rentabilidad cae hacia la media

· Si r_t < r* entonces ∆r > 0: la rentabilidad sube hacia la media

· Si r_t = r* entonces ∆r = 0: la rentabilidad se estabiliza

· Β es la velocidad de ajuste de la rentabilidad, similar al coeficiente α

La podemos reorganizar de la siguiente forma:

Por lo tanto:

Si β es igual y superior a 1, el sistema divergirá, este es un comportamiento que puede darse en períodos determinados, por ejemplo en momentos de burbuja o sobrecalentamiento de la economía, pero a largo plazo β debe poseer un valor superior a 0 e inferior a 1. En tal caso, el sistema se estabilizará conforme t tienda a infinito al valor de equilibrio:

Por lo tanto, en el largo plazo la rentabilidad tiende al equilibrio de la rentabilidad media de la economía.

Se puede contestar que la realidad de una economía no es a la competencia perfecta, lo cual es correcto, pero este modelo no explica ni se fundamenta en los mismos principios de la competencia perfecta, es por el contrario, un modelo que coincide con la idea de coincidencia más amplia presente incluso en modelos analíticos marxianos y austriacos, por lo que no se entiende estáticamente y sí dinámicamente. Los monopolios se pueden formar, pero no es parte de la naturaleza económica su consolidación sino su destrucción conforme la competencia se instala.

5) Restricciones no convexas

La existencia de restricciones no convexas impide la optimización tal y como se presentó, esto pues si la región no es convexa, el óptimo (mínimo o máximo) no necesariamente es global, lo que, de aceptarlo, nos da como resultado un uso no-óptimo de los factores, al menos entendiendo que no se está escogiendo un punto de optimidad global.

Para entenderlo observemos la siguiente representación:

La función objetivo es una parábola invertida con máximo global en el punto rojo: (2, 2), la región factible es la unión de dos círculos separados (verde en el gráfico a la izquierda). El óptimo en un caso es el punto (1,1) y en otro (3,3), sin embargo, como se observa en el gráfico a la derecha, ninguno de ellos es el óptimo global (2,2).

Otro ejemplo para entender mejor este problema es el siguiente:

La función a optimizar es convexa y la región factible cóncava con dominios separados. Los mínimos marcados por los puntos verdes son mínimos locales en tanto el mínimo global se encuentra fuera de la región factible.

Pero incluso en estas circunstancias, obsérvese que existen óptimos que, razonamiento económico mediante, dirigen las diferentes asignaciones de recursos. La presencia de restricciones no convexas no elimina la existencia de una solución óptima. Aunque impide aplicar directamente métodos analíticos como KTT, no suprime la racionalidad económica ni la tendencia estructural hacia la eficiencia en el uso de recursos. Los agentes, enfrentados a restricciones discretas, tecnológicas o institucionales, adaptan su comportamiento mediante métodos alternativos —como enumeración, simulación, heurísticas o programación entera— que les permiten aproximarse o alcanzar el máximo beneficio posible. Por tanto, la no convexidad representa una dificultad técnica, pero no una barrera insalvable para la optimización económica.

Pongamos de ejemplo los casos más representativos de áreas factibles no convexas:

Que representan los siguientes escenarios:

· Inversión en proyectos mutuamente excluyentes

· Restricciones tecnológicas con saltos

· Inversión sujeta a umbrales regulatorios

· Restricciones geográficas, políticas o logísticas

En todos estos casos estamos en situaciones en las que no hay continuidad ni soluciones intermedias. Pero aun así, es posible optimizar la decisión, por ejemplo ante dos opciones mutualmente excluyente, es posible analizar el VAN de cada opción y proceder con la comparación con el objetivo de tomar la decisión más factible de cara al inversor.

Es decir,

Es decir, si VAN_A > VAN_B la inversión A será elegible en contraste a la inversión B, y esto es aplicable incluso (y mejor dicho, especialmente) a los casos anteriormente mencionados.

La demanda

Llegados hasta aquí, hemos trabajado únicamente desde el lado de la oferta empresarial, de sus decisiones y del cómo las optimiza con el fin de invertir el máximo en los factores productivos con tal de maximizar el beneficio, sin embargo hasta ahora hemos ignorado la demanda, la cual puede variar y incrementarse (o reducirse) generando con ello un incremento del margen de beneficio empresarial.

Para que se entienda lo representamos a continuación:

La desviación total es la diferencia entre el beneficio neto real y el beneficio neto presupuestado. La cual se puede desglosar como sigue:

Donde el primer sumando es la desviación en márgenes y el segundo es la desviación en cantidades.

La desviación en márgenes, a su vez, puede descomponerse del siguiente modo:

Donde:

Es la desviación en precios y:

Es la desviación en costes variables.

Si denominamos Q a las ventas totales del conjunto de empresas que compiten en el mercado y t a la proporción de las mismas correspondiente al producto en cuestión, como será obvio: q = tQ

Y por lo tanto la desviación en cantidades puede descomponerse en:

Donde el primer sumando es la desviación en cuotas:

Y el segundo la desviación del tamaño global del mercado:

Por lo que podemos sintetizar este análisis en que, la desviación de los márgenes totales (hacia el alza o baja) se puede producir por:

1. Una desviación de márgenes. Estas a su vez se pueden derivar de una desviación de precios o una desviación de costes.

2. Una desviación de cantidades. Las que se derivan de una desviación en cuotas o una desviación en el tamaño del mercado.

Por lo cual el incremento de la demanda puede incrementar las ganancias de una empresa, lo que podría justificar un incremento de salarios con el fin de aumentar la demanda interna y con ello las ventas: más cuotas o mercado para que las empresas incrementen sus márgenes.

No obstante, en términos sectoriales esto puede ser cierto, pero en términos agregados la desviación en márgenes y la desviación en cantidades tenderán a anularse ante un incremento de salarios y demanda.

En términos matriciales se puede expresar como sigue:

En términos matriciales;

Simbólicamente; X = AX + D

Donde X es la producción, AX la demanda interindustrial y D la demanda final.

El modelo de Leontief supone que todo cuanto se produce se usará, es decir, que la producción es igual a la demanda. En estas condiciones el modelo pretende determinar cuánto debe producir cada industria para que haya un equilibrio entre la oferta y la demanda.

Suponiendo que la matriz (I-A) tiene inversa, podemos resolver este sistema despejando X:

La inversa de Leontief se utiliza en el análisis input-output de la economía para determinar cómo los cambios en la demanda final de bienes o servicios afectan la producción total necesaria en todos los sectores. Específicamente, permite calcular la cantidad total de insumos directos e indirectos que cada sector debe producir para satisfacer una determinada demanda final, considerando las interdependencias entre sectores. Por ejemplo:

En este caso, AX+C nos da como resultado X.

Y a la vez, (I – A) ^-1*C da como resultado X.

Así, la matriz inversa de Leóntiev refleja el efecto multiplicador de la producción en la economía.

Usándola, podemos calcular coeficientes y niveles de producción por sector en una economía, pero además todo este análisis nos permite extendernos a otra conclusión todavía más general: el nivel de producción debe ser igual al nivel de demanda interindustrial más la demanda final.

Por lo que esta igualdad nos permite entender por qué no es posible, a nivel agregado, incrementar la demanda sin afectar la oferta en un sentido no perjudicial. Es decir, la matriz D puede aumentar, o disminuir, autónomamente solo cuando hablamos de un sector determinado de la economía, en agregado además de una equivalencia existe una relación de dependencia desde la inversión hacia la demanda.

Una síntesis

Hasta aquí, nos hemos centrado exclusivamente en una simple idea: el monto del beneficio empresarial no se fija arbitrariamente al margen de factores económicos y sociales, leyes que explican el comportamiento del mercado, al contrario, el margen del beneficio empresarial está justamente dado una vez una serie de factores se encuentran igualmente dados. Por lo que una tendencia a pagar menos para obtener más beneficio por el mismo trabajo no debiera tener sentido en contextos de competencia y optimización de la producción.

Resumiendo la idea defendida:

- Beneficio empresarial: Ingresos – costos fijos y variables (entre ellos, el salarial)

- El monto del beneficio salarial, en términos del total de la producción, se incrementa (o reduce) en la medida en que se reducen (o aumentan) los costos.

- La distribución anterior no es arbitraria, no depende solo y únicamente de la decisión del empresario, al contrario, esta se somete a condiciones objetivas impuestas por el mercado.

- La inversión en los factores productivos se rige por el principio de la maximización y optimización del resultado.

Por lo tanto, asumamos los siguientes escenarios:

Primero, un empresario decide incrementar arbitrariamente el monto del beneficio mediante reducciones nominales y reales del salario de sus trabajadores.

Segundo, los empresarios de un sector ven incrementado el monto de su beneficio debido a una reducción del impuesto directo aplicado a sus beneficios.

Tercero, los empresarios introducen innovaciones técnicas que conllevan en la duplicación de la productividad del trabajo lo cual les permite reducir los costes e incrementar el beneficio.

Lo interesante de estos escenarios, es que la acusación de los círculos de izquierda (Iglesias, Navarro, y otros) solo tiene sentido una vez se entiende la forma precio como una suma de partes (costos no salariales + costos salariales + beneficio) que se pueden alterar como ceteris paribus manteniendo un equilibrio predefinido. Es decir, la idea básica que subyace detrás de estas lecturas se resume en creer que, en el caso de que el precios sea 1000 u.m. equivalente a 500 u.m. de costos no salariales, 200 u.m. de costos salariales y 300 u.m. de beneficios, podré reducir 50 u.m. los costos salariales e incrementar a 350 u.m el beneficio. Al contrario, desde una perspectiva marxista y neoclásica, esto no ocurre. En el primer caso porque el precio, si bien es cierto no es igual al valor, sí gira en torno a éste en una relación gravitatoria, por lo cual la explicación final y determinante son los tiempos socialmente necesarios empleados en la producción de bienes reproducibles a escala. En el segundo caso, el precio se explica por una compleja relación de utilidades marginales, individuales y subjetivas de los individuos que participan en el mercado interactivamente segundo a segundo. Profundicé esto en mi artículo anterior sobre el salario mínimo.

En el primer caso, la tasa de beneficio aumentará en la empresa A, que es la empresa cuya mesa directiva arbitrariamente decidió reducir los salarios como manera de competir, sin embargo si el salario que ahora oferta la empresa no compensa el costo de oportunidad de la población económicamente activa, estos individuos podrían decidir dejar de ser económicamente activos o postular a empresas donde los salarios ofertados sean más elevados. El empresario de la empresa A ha decidido pagar menos, pero no ha modificado las utilidades y preferencias individuales que cada individuo posee a la hora de decidir trabajar o no trabajar.

Si, incrementar el margen de beneficio fuera tan simple, las empresas que utilizan mano de obra cualificada podrían remunerar con salarios de igual o similar monto a las empresas que utilizan mano de obra no cualificada sin mayores problemas, lo cual no es lo que acontece, y sobre esto tenemos ejemplos históricos y experimentos a gran escala como lo que ocurre día a día en sociedades con escalas salariales muy desequilibradas -al menos- comparadas con nuestras escalas salariales.

En el segundo caso, pasamos de la decisión de un empresario particular, al incremento del beneficio de un sector completo (por ejemplo, el automovilístico). En este caso la competencia aplica. En la medida que exista una libertad para invertir y desinvertir, los capitales tenderán a moverse, con el tiempo (no necesariamente el cambio es inmediato, como ya se analizó) a los sectores más rentables, por lo que incluso cuando un grupo de empresarios dueños del 80% de un sector determinado decidan reducir los montos salariales con el objetivo de incrementar sus beneficios, el efecto derivado de la competencia generará una mayor inversión y demanda de trabajadores lo que, con el tiempo, tenderá a incrementar los salarios reales de los mismos.

En el tercer caso, al existir un incremento de la productividad por trabajador dentro de una economía, eventualmente si el incremento salarial es inferior al incremento de la productividad, el beneficio tendería a aumentar, pero esto no significa que el salario no se incremente, significa que podría incrementarse menos que el valor añadido por trabajador. Habrá otros factores que expliquen la dinámica, pero aun cuando el salario aumente menos que la productividad, por efectos de la competencia (al incrementarse el beneficio) la demanda del trabajo aumenta y con ello también el salario de los trabajadores, por eso existe una alta correlación entre el valor añadido por trabajador y los salarios reales en las sociedades y, por lo mismo, en países con mayores niveles de productividad por hora laboral o PIB por ocupado, los salarios igualmente son mayores.

La situación española

Llegados a este punto, al menos teóricamente, se ha contestado los principales argumentos de Iglesias, Navarro y compañía, pero para cerrar con un candado argumentativamente sólido el presente artículo, me gustaría evidenciar cómo, a diferencia de lo que explican, el incremento continuo de los beneficios o excedentes no es el que explica los graves problemas del mercado del trabajo. La idea de divergencia entre productividad y salarios reales no explica la situación social española.

Primero que todo, es preciso exponer el anómalo comportamiento de la productividad, la ocupación y los salarios reales en España. Esto pues, en términos generales dentro de la OCDE, la tendencia suele ser una alta correlación (coeficiente r² superior a 0,8) entre todos estos indicadores, es decir, conforme la productividad crece, también lo hacen los salarios reales y la ocupación, sin embargo en el caso español lo que ha ocurrido entre los años 2000 y 2008 es lo expuesto en el siguiente gráfico:

La curva que correlaciona la productividad y los salarios reales es cóncava, tiende a crecer hasta un punto, luego se estanca y posteriormente comienza a reducirse. Llegado a un punto, los incrementos de productividad por trabajador en la economía española se daban a la par de reducciones en los salarios reales. Por otra parte, la curva que explica la relación entre productividad y ocupados tiene un primer tramo cóncavo y un segundo tramo convexo. Inicialmente el crecimiento de la productividad se daba a la par de un incremento de los ocupados hasta llegado un punto en que esta relación se estanca, procediendo a su reducción hasta que la tendencia (años 2012 y 2013) se invierte y los incrementos de productividad se manifiestan con incrementos en la tasa de ocupación.

Si invertimos los ejes y la productividad la ubicamos en el eje de ordenadas, podremos observar con más detalle el problema.

En relación con los salarios reales: los salarios crecen mediante estancamiento de la productividad y se reducen cuando esta se incrementa.

En relación con la ocupación: la productividad se estanca cuando la ocupación crece (años 2000 – 2007 y luego 2013 – 2019/2020) y se incrementa cuando la ocupación se estanca (años 2008 – 2013).

Pareciera como si hace ya muchos años la economía española hubiese llegado a un tope de productividad y que por ende ahora, cuando se requiere elevar la productividad, se haga por la vía de reducir el número de trabajadores ocupados y por el contrario, si se necesita aumentar la producción se haga reduciendo la productividad (o manteniéndola muy estancada).

Generalmente las funciones de producción poseen rendimientos decrecientes, por lo que una vez no hay aumentos significativo de producción cuando se incrementan los factores productivos, se imponen renovaciones tecnológicas que permiten incrementar la productividad, pero en este caso lo que observamos es que al menos durante 20 años no se ha solucionado el problema por la vía de la innovación.

¿Cuál es el problema de la economía española que no da ese salto cualitativo?

Para contestar esta pregunta, vamos a proceder con una teoría explicativa.

En condiciones de libertad económica, las empresas tenderán a maximizar su beneficio mediante la inversión y desinversión entre los diferentes sectores así como también modificando la composición y el stock de sus factores productivos. A saber, como ya se indicó, si hay diferenciales en el beneficio por sector, las inversiones tenderán al sector más rentable hasta que estas diferencias se reduzcan al mínimo. Lo mismo aplica en caso de que el costo del factor trabajo (o cualquier otro factor) sea muy elevado, en este caso se optará por vías que permitan reducir el mismo, ya sea incrementando la productividad o reduciendo el número de ocupados. En este sentido, reducir el número de ocupados solo sirve cuando nos encontramos en periodos de recesión, en otros casos la norma es a incrementar las tasas de ocupación en medio de la competencia entre empresas, por lo que obtener mayores tasas de beneficio se conseguirá generalmente por la vía de la innovación. Esto significa que, además de tender al crecimiento de la productividad por trabajador, las economías en condiciones de libertad económica tenderán a bajos niveles de desempleo, y esto último es lo que no ocurre en España.

Si la economía fuera cerrada, los únicos factores a considerar serían los costos internos de la misma, mas en condiciones de economía abierta, los costos internos deben analizarse en relación a los costos del resto de la comunidad. El punto es que no solo importa si los salarios, cotizaciones, impuestos y otros costos son altos o bajos en comparación al pasado o en relación al nivel productivo, además es importante tener en cuenta si estos costos son mayores, menores o los mismos en comparación a otros países cuyos niveles de renta, productividad y desarrollo son similares a los nuestros. Si por ejemplo, reducimos los costos de producción un 15% en un lapso de 10 años, y a la vez los países vecinos los reducen un 20% en el mismo período, nos habremos convertido en una economía un 5% más costosa de cara al empresario. Y si estos vecinos son capaces de ofertar similares ventajas, entonces la opción a la hora de invertir será a la desinversión de nuestra economía.

Una forma de ver esta situación es analizando los costos laborales.

En estos gráficos (que presentan la misma información con la diferencia en que el segundo acota su rango para ver con mayor claridad la distribución de los países) podemos observar el cambio acumulado entre el valor añadido y la compensación por trabajador entre los años 2000 y 2023. La recta que cruza diagonalmente tiene un ángulo de 45º y marca la diferencia entre los países que han expuesto un desplante en el que el crecimiento de la productividad ha sido superior (bajo la recta) o inferior (sobre la recta). Países como Polonia o Irlanda han visto su productividad incrementada en una proporción superior al crecimiento de los costos. En cambio otros, como Letonia, han visto incrementados sus costos salariales en mayor proporción que la productividad. Quitando estos casos más llamativos, el grueso de los países se ubica cerca de la recta, entre ellos España.

Si contrastamos el cambio neto (diferencia entre incremento de productividad y compensación laboral por hora), donde el valor más bajo significará un peor rendimiento a medio plazo, el resultado (como se observa en el siguiente gráfico) es que España se encuentra por debajo de la media del área euro, Portugal, Estados Unidos, Alemania y otros países. No es el país con el peor desplante, pero sí que se encuentra en la mitad con peor rendimiento (de 37, 21 presentan mejor desenvolvimiento).

Si nos centramos en el 2023 y comparamos la proporción de la compensación laboral en el valor añadido por trabajador, podemos observar que España solo es superada (mayor nivel de compensación por productividad) por 11 países (de 40). Es decir, producir en España es relativamente caro incluso comparada con los países de la zona.

Si contrastamos esta información con la diferencia de las dinámicas entre 2000 y 2020 podemos agrupar los países en cuatro grupos: a) países que son menos costosos que la UE y la dinámica fue positiva, b) los países que son menos costosos que la UE y la dinámica fue negativa, c) los países que son más costosos que la UE y la dinámica negativa, d) los países más costosos que la UE y la dinámica positiva.

En el primer grupo tenemos a países como Estados Unidos, Israel, Noruega, Canadá. En el segundo a Letonia, Lituania. En el tercero a Bulgaria, Estonia. Y en el cuarto a España o Bélgica. Si bien es cierto, España no se encuentra en el peor grupo, la comparación y el análisis se vuelve mucho más pesimista cuando incluimos el PIB per cápita tal y como se observa a continuación:

El costo relativo a la productividad por hora trabajada en España a nivel de PIB per cápita solo es igual o inferior a unos pocos países de la región, entre los que se incluyen Croacia o Bulgaria, sin embargo el mismo es igual o superior a un gran número de países tan o más ricos (como Israel, Noruega, Estados Unidos, Canadá, Reino Unido). Por lo que España es un país más costoso y menos productivo que buena parte de la comunidad internacional y, especialmente, con buena parte de la comunidad económica con quien comparte lazos comerciales y económicos de intensa profundidad.

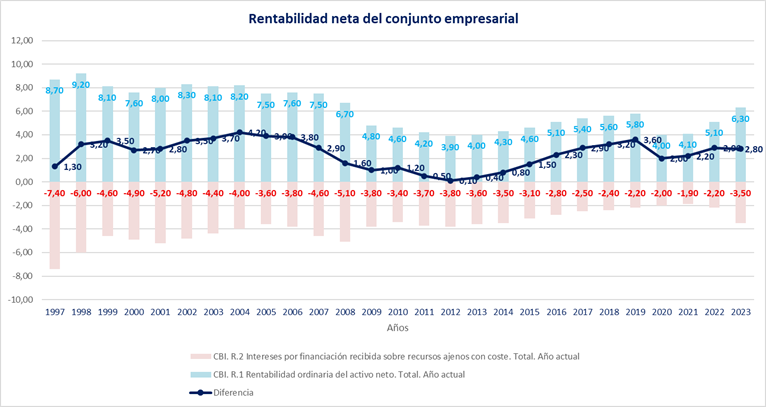
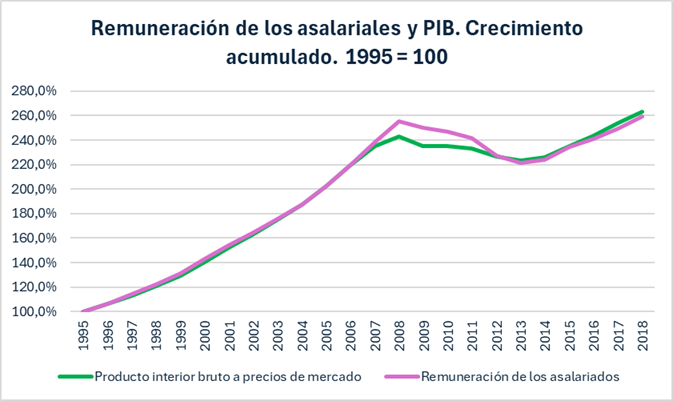
Además, la rentabilidad neta se ha mantenido estancada por debajo de los niveles de inicios de siglo a pesar de los ajustes realizados durante el gobierno del Partido Popular liderado por Mariano Rajoy. Esto se debe a que a pesar de que desde 2012 en adelante el PIB ha crecido más que la remuneración de los asalariados (hasta 2020), la intensa divergencia entre remuneraciones y PIB dada entre 2005 y 2011 no ha sido totalmente revertida.

Por otra parte, los costos impositivos son significativos.

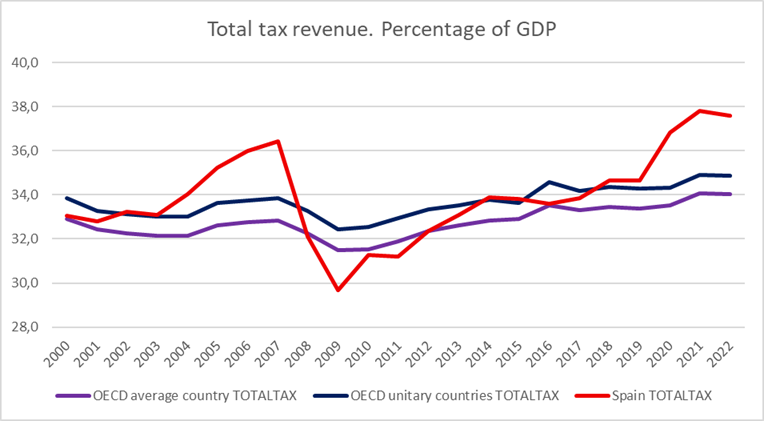
La presión fiscal en España se ha incrementado continuamente desde el año 2009. Dentro de los países OCDE, España es uno de los que cobra un nivel mayor de impuestos corporativos.

El peso de los impuestos sobre las ganancias del capital es significativamente superior en España, lo mismo cabe a las cotizaciones sociales.

La estructura impositiva española se caracteriza por una notable falta de competitividad en el contexto europeo, derivada principalmente de la elevada carga de las cotizaciones sociales, que alcanzan el 36.3% del salario bruto, y un impuesto de sociedades con un tipo nominal del 25%, situado en la media-alta de la UE. Esta dependencia de las cotizaciones, que representan un 12.7% del PIB, y la presión fiscal sobre las empresas limitan el atractivo de España para la inversión extranjera y la contratación, especialmente frente a países como Irlanda (14.8% en cotizaciones y 12.5% en sociedades) o Hungría (28.3% y 9%, respectivamente). Aunque la presión fiscal total (33.8% del PIB) es inferior a la media europea, su distribución desequilibrada, con un peso excesivo en el empleo y las empresas, en lugar de diversificarse hacia impuestos como el IVA o el IRPF, restringe la capacidad de España para competir con economías de menor carga tributaria y mayor flexibilidad fiscal, como los países del Este o los hubs financieros de la UE.

Si el costo sobre el capital es elevado, ¿qué ocurre con el costo sobre el trabajo? Pues depende. España es uno de los países con mayores costos al despido, lo que se traduce en un mercado laboral rígido, derivado de ello la capacidad para crear empleo formal se ha mantenido constreñida.

Por otra parte, el flujo de inmigración ha seguido manteniéndose en positivo desde la crisis financiera e inmobiliaria. La correlación expuesta es negativa, por lo que a priori se podría establecer como conclusión que la llegada de inmigrantes ha fomentado e incentivado el desarrollo de sectores económicos de bajo valor agregado.

Si la economía española ha mantenido un ritmo positivo de crecimiento ha sido, en buena medida, por el flujo de inmigrantes que ocupan puestos de trabajo de bajo valor añadido.

Todos estos problemas se han traducido en un desplante negativo de la PTF española (2000-2022).

Este indicador es expresión máxima de la debilidad empresarial española en torno a la capacidad para crecer, generar empleo y sobre todo mantener un ritmo de crecimiento cualitativo a largo plazo.

Desde una perspectiva estructural, los jóvenes constituyen el grupo poblacional más expuesto a las rigideces y desequilibrios del mercado laboral español. Su inserción se ve obstaculizada por una combinación de factores: elevada temporalidad en los contratos, alta tasa de desempleo juvenil, escasa correlación entre cualificación y demanda efectiva de trabajo, y restricciones normativas que penalizan la contratación indefinida. Estas condiciones no solo implican un menor ingreso laboral en las etapas iniciales del ciclo vital, sino que además deterioran la acumulación de capital humano específico, la estabilidad contributiva al sistema de pensiones y la movilidad intergeneracional. En contextos donde la estructura productiva no logra absorber eficientemente el incremento de oferta laboral joven, y donde los márgenes empresariales están constreñidos por rendimientos decrecientes o baja productividad, el resultado es un desequilibrio persistente en la transición al empleo formal. En este sentido, el subempleo juvenil actúa como un indicador adelantado de las disfunciones sistémicas del aparato productivo, y exige reformas orientadas no solo a flexibilizar la contratación, sino también a reestructurar los incentivos formativos, tecnológicos y fiscales que condicionan la demanda agregada de trabajo cualificado.

Conclusión

En definitiva, aunque es indudable que las grandes empresas españolas han mantenido niveles significativos de rentabilidad incluso en contextos de crisis, atribuir de forma unívoca los problemas del desempleo y la precariedad laboral a esta realidad resulta reduccionista. El comportamiento empresarial, como se ha demostrado a lo largo de este trabajo, está profundamente condicionado por estructuras de costes, restricciones tecnológicas, dinámicas de competencia e interacciones globales que limitan su capacidad para actuar de forma arbitraria o unívoca. Asimismo, factores como la rigidez del mercado laboral, la estructura productiva de bajo valor añadido, los incentivos fiscales desalineados y las tendencias demográficas configuran un ecosistema económico más complejo que el señalado por algunas corrientes de crítica ideológica. Superar los desafíos estructurales del empleo en España requiere un enfoque integral que combine eficiencia productiva, dinamismo innovador y políticas públicas equilibradas, sin caer en simplificaciones que sobredimensionen el margen de acción de las empresas o desconozcan las condiciones objetivas del mercado.